今天來跟著助教看看快速傅立葉轉換吧！
就直接上程式碼：

import numpy as np
import matplotlib.pyplot as plt

#定義計算二進制的位元反轉函數
def bit_reversal(number, bitsize): 
    binary = bin(number) #將整數轉換為二進制表示
    reverse = binary[-1:1:-1] #反轉二進制數的順序（不包括 0b 前綴）
    reverse = str(reverse)+"0"*(bitsize-len(reverse)) #如果反轉後的長度不足 bitsize，則補零
    return int(reverse, 2) #將反轉後的二進制數轉為整數
    
#定義根據蝴蝶圖進行數據合併的FFT_unit函數
def FFT_unit(array_e, array_o): #array_e和array_o 分別是原始數據中所有偶數和奇數索引的位置
    N = len(array_e)*2 #將一個長度為 N 的陣列拆分成兩個長度為 N/2 的陣列進行處理
    W_array = np.array([np.exp(complex(0, -2*np.pi*a/N))for a in range(int(N/2))]) #製作傅立葉變換中的旋轉因子
    output1 = array_e + W_array*array_o #數據合併結果
    output2 = array_e - W_array*array_o #數據合併結果
    return np.hstack((output1, output2)) 

#定義一維快速傅立葉變換函數
def FFT_1D(array_i): #array_i為狹縫空間域數據
    length = len(array_i)  #取 array_i 的長度，得輸入數據的總數量
    bit_size = int(np.log2(length)) #計算輸入數據長度的對數（以 2 為底），即 log2(length)，用來確定位反轉(bit reversal)所需的位數
    rearrange = [] #初始化一個空列表，稍後將用來存放經過位反轉後重新排列的數據
    for i in range(length): 
        bit_reverse = bit_reversal(i, bit_size) #計算i 的位反轉結果。例: i 是二進位的 001（十進位為 1），在三位的情況下，它的位反轉結果是 100（十進位為 4）
        tmp_array = np.array([array_i[bit_reverse]]) #根據位反轉後的I，從 array_i 中取出對應的元素，並將其轉換為一個array
        rearrange.append(tmp_array) #將重新排列的array加入到 rearrange 列表
    output = rearrange
    for s in range(bit_size): #以外部迴圈控制 FFT 的計算層數（每一層的計算都相當於蝴蝶圖中的一層操作)
        tmp_list =[] #初始化一個空列表
        for j in range(int(len(output)/2)): #遍歷目前數據的1/2
            tmp_array = FFT_unit(output[2*j], output[2*j+1]) #帶入FFT_unit對數據執行蝴蝶操作，產生新的頻域數據
            tmp_list.append(tmp_array) #將數據的運算結果加入到 tmp_list 中
        output = tmp_list
    return output[0] #得最終的計算結果

# 定義單狹縫
def slit(x, w):
    if (D/2-w/2) < x <= (D/2+w/2):
        return 1/w
    else:
        return 0

# 設定解析度、空間範圍、狹縫寬度
N = 512
D = 10
K = N*2*np.pi/D
w = 1

# 設定空間變數的列表
x_list = [i*D/N for i in range(N)]
kx_list = [i*K/N for i in range(N)]

# 計算狹縫函數及其FFT
slit = [slit(x_list[i], w) for i in range(N)]
FFT_slit = FFT_1D(np.array(slit))

# 畫圖
plt_phi1 = [slit[i] for i in range(N)]
plt_phi2 = [abs(FFT_slit[(i+int(N/2))%N])/N for i in range(N)] #帶入單狹縫函數並取絕對值得光強
plt.subplot(1,2,1)
plt.plot(x_list, plt_phi1, label= 'slit')
plt.legend()

plt.subplot(1,2,2)
plt.plot(kx_list, plt_phi2, label= 'FFT1D')
plt.legend()
plt.show()

得出圖如下：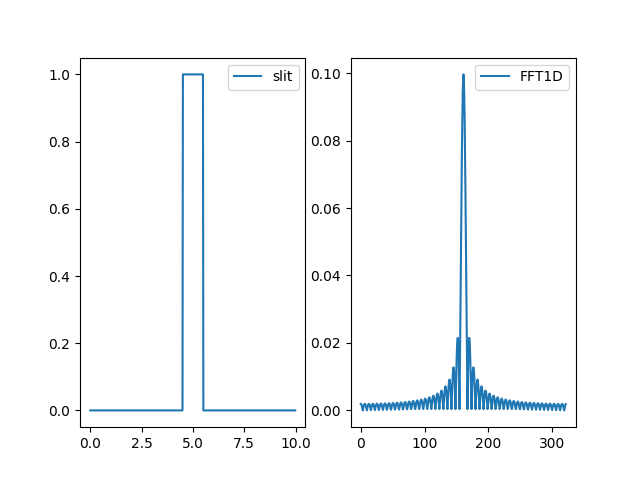

右圖可以看到用快速傅立葉轉換計算的一維單狹縫繞射，把昨天的離散傅立葉轉換拿過來比一下：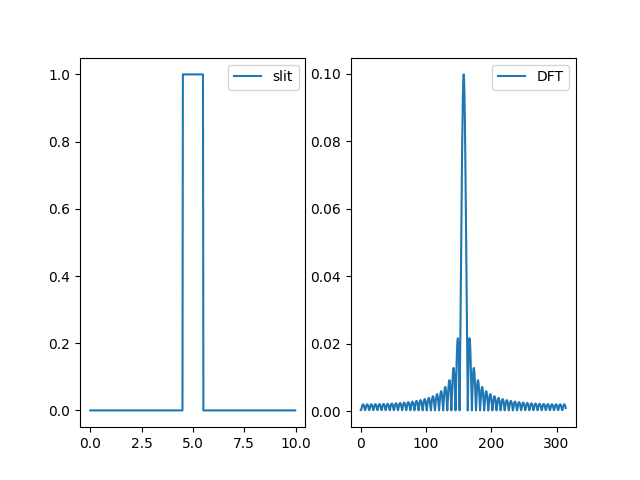

近似結果非常相近，來問問看chatGPT有什麼不同好了：

離散傅立葉轉換和快速傅立葉轉換在理論上應該產生相同的頻譜結果，但由於 FFT 是一種更高效的計算方法，它可能會更快地得出結果，並且在實際應用中數值誤差也可能略有不同。然而，這些差異對最終的頻譜分析影響非常小，在大多數情況下可以忽略不計。

這裏再請chatGPT幫我補一下FFT中一些知識：

何謂蝴蝶圖 (Butterfly Diagram)？
蝴蝶圖是 FFT 運算中的一個視覺化工具，用來表示 FFT 的遞迴合併過程。它形象地展示了數據如何通過多次分割與合併，最終完成傅立葉變換的過程。

在蝴蝶圖中：

1. 分割：原始數據按照偶數和奇數索引位置分成兩組。
2. 旋轉因子：每一組數據會乘以一個複數旋轉因子，這個旋轉因子是由傅立葉變換中的指數項計算得出的。
3. 合併：通過一個類似蝴蝶形狀的操作，兩組數據再重新合併成一組數據。
   這個過程不斷重複，直到最終得到傅立葉變換的結果。因為每個數據點的處理過程在圖形上看起來像一個展翅的蝴蝶，所以稱為蝴蝶圖。

看到這邊不知道大家有沒有注意到，昨天和先前的取樣點的數量（細緻度）N 都是 501，但是今天的FFT中N設定為512。
這就與蝴蝶圖有關了！由於會不斷分成兩組旋轉處理，數據的數量也被限定在2 powers，所以只好採用接近501的512(2的9次方)

老實說這邊助教教的真的有點太難了，雖然配著AI免強啃得下去，但要自己寫出來還是有點難度ＱＱ
今天就到這裡，好好休息，謝謝助教和AI！